1 Scope

Occasionally, I receive e-mails with cries for help with R and, more specifically, R 'Luminescence'. Usually, the questions are very task-tailored and come with their datasets to reproduce the problem; so there is nothing I can share. However, some questions address more general issues. Then, I always think it would be nice to write a tutorial about it, but I usually never do because this is rather time-consuming. The latest request I received was slightly different because this question was asked a few times, and the answer is indeed very straightforward to give. So, let’s summarise it in a little tutorial for future usage.

The assignment at hand is to analyse (single-grain OSL) data using the finite mixture model (FMM, cf. Galbraith and Roberts, 2012) and then visualise the results nicely in an Abanico plot (Dietze et al., 2016). Admittedly, what I will present in the following is already available to some extent in the supplement to Dietze et al. (2016). Still, it appears not many people were looking into it.

2 Data generation

For our purpose, it is easiest to generate the dataset we need to analyse ourselves. In reality, it will be a dataset measured in the luminescence laboratory using a single-grain attachment or a camera.

Our dataset will have three different dose components, each following a normal distribution. The individual uncertainties are also sampled from a normal distribution representing relative uncertainties.

## set random seed for reproducibility of this example
set.seed(1362023)

AGE <- c(rnorm(30, 30, 2), rnorm(30, 45, 5), rnorm(30, 50, 2))
AGE_X <- AGE * rnorm(90, 0.07, 0.02)

## combine to data.frame
df <- data.frame(AGE, AGE_X)

## show as KDE plot
Luminescence::plot_KDE(df)

3 Data analysis and plotting

Although we have just created the dataset, we now treat it as an unknown and run the FMM analysis to identify the statistically most meaningful number of dose components in the dataset. Use the Luminescence::calc_FiniteMixture() this can be done by letting the number of components free float between 2 and, here arbitrarily selected, 5.

Luminescence::calc_FiniteMixture(
  data = df,
  sigmab = 0.01,
  n.components = 2:5)

## 
##  [calc_FiniteMixture]
## 
## ----------- meta data ------------
##  n:                     90
##  sigmab:                0.01
##  number of components:  2-5
## 
## -------- single component --------
##  mu:                     41.4464
##  sigmab:                 0.01
##  llik:                   -520.449
##  BIC:                    1045.3979
## 
## ----------- k components -----------
##             2     3     4     5
## c1_dose 30.43 30.38 30.38 30.05
## c1_se    0.34  0.35  0.35  0.66
## c1_prop  0.36  0.35  0.35  0.30
## c2_dose 47.81 39.43 39.02 32.64
## c2_se    0.36  0.95  0.93  2.94
## c2_prop  0.64  0.06  0.03  0.05
## c3_dose  <NA> 49.57 46.23 39.10
## c3_se    <NA>  0.45  1.27  0.89
## c3_prop  <NA>  0.59  0.23  0.03
## c4_dose  <NA>  <NA> 50.86 46.22
## c4_se    <NA>  <NA>  0.71  1.27
## c4_prop  <NA>  <NA>  0.38  0.23
## c5_dose  <NA>  <NA>  <NA> 50.86
## c5_se    <NA>  <NA>  <NA>  0.71
## c5_prop  <NA>  <NA>  <NA>  0.38
## 
## ----------- statistical criteria -----------
##           2       3       4       5
## BIC  25.684 -65.047 -61.540 -53.577
## llik -6.092  43.773  46.519  47.038
## 
##  Lowest BIC score for k = 3
##  No significant increase in maximum log likelihood estimates.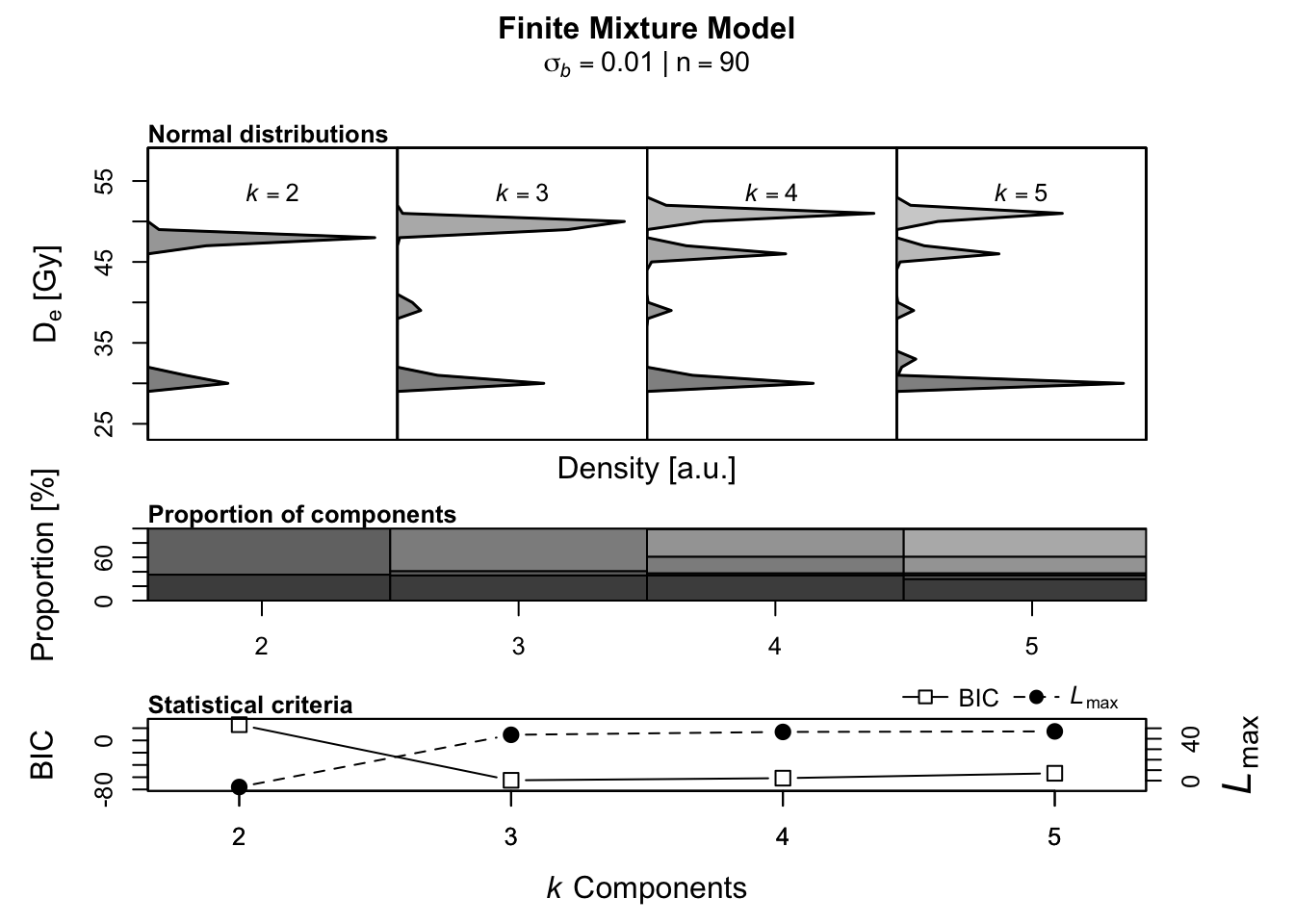

From the analysis, we can deduce that the most meaningful number of components of our “unknown” dataset is 3. Every additional component is statistically not justified. After this initial inspection of the data, we rerun the analysis with the number of components fixed to 3 and the output stored in an object called FMM, which will come in handy for the plotting. I use the option verbose = FALSE here to suppress the terminal output, which is not required here.

FMM <- Luminescence::calc_FiniteMixture(
  data = df,
  sigmab = 0.01,
  n.components = 3, 
  verbose = FALSE)

In the following, I first generate the plot and then explain the applied settings below.

Luminescence::plot_AbanicoPlot(
  data = df, 
  summary = c("n"), 
  rug = TRUE, 
  bar = FMM$summary$de,
  bar.col = adjustcolor(
    khroma::color(palette = "bright")(), alpha.f = 0.4),
  polygon = FALSE, 
  line = FMM$summary$de,
  line.lab = paste0(
    round(FMM$summary$de,1), " ± ", round(FMM$summary$de_err,1)), 
  main = "FMM results")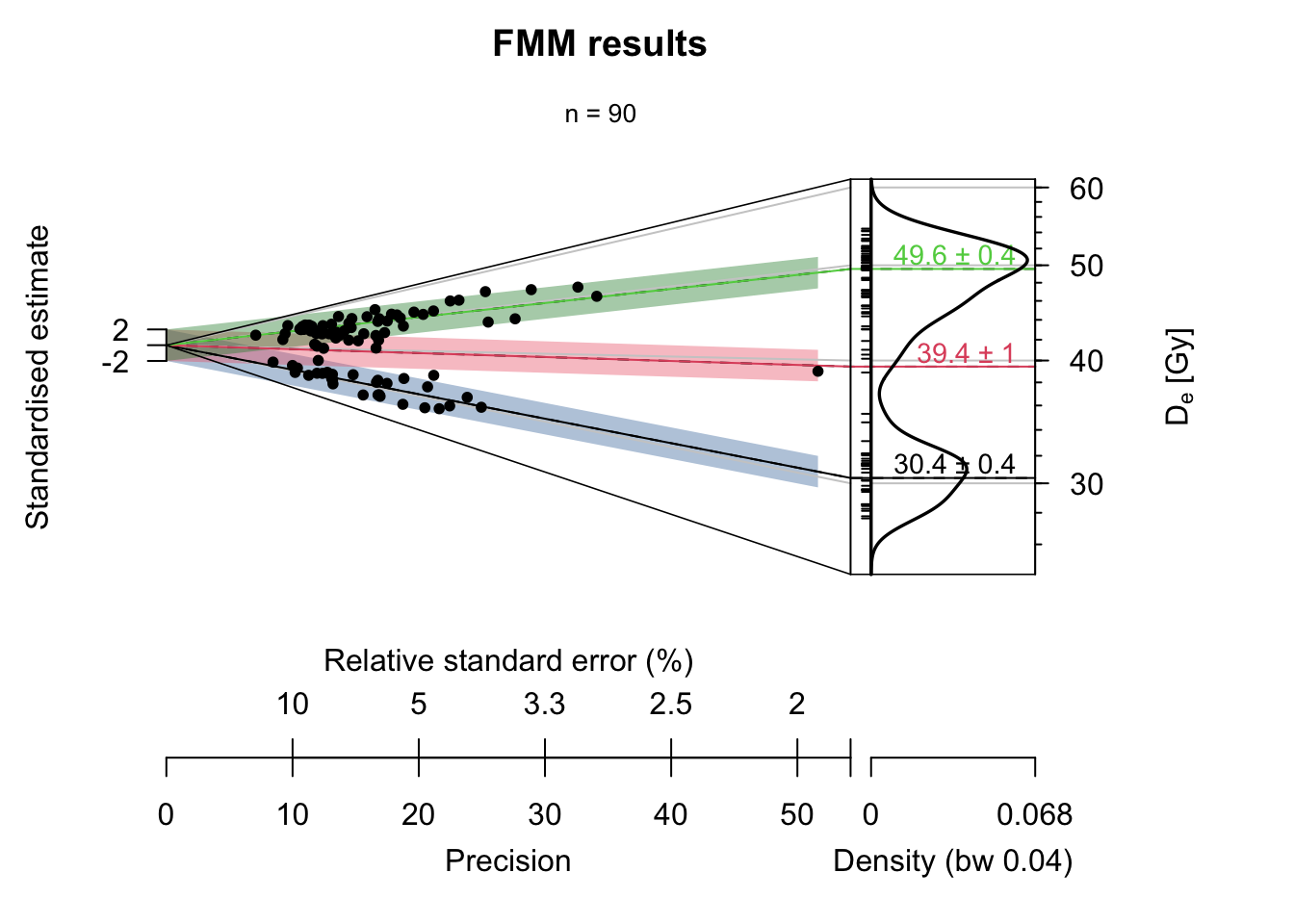

• data as input, we set the data.frame with the “measured” values
• summary will display only the number of observations; therefore, we set it c("n")
• rug displays the small ticks along the vertical; this is not needed but nice to have
• bar has as input the identified components, and it will generate the 2-sigma polygons
• bar.col sets the colour of the 2-sigma bars. For the colour palette we use the R package khorma by Nicolas Frerebeau because it provides nice colours for colour-blind persons. The adjustcolor() call is used only to render the colours a little bit transparent
• polygon removes the two standard deviations grey area from the plot, which is unnecessary in our case but would be more like chart junk.
• line adds centre lines to each component and connects it with the kernel density part of the Abanico plot
• line.lab adds labels to the components, which we set to the identified component central value
• main sets the title of the plot

The plot can be further modified, but the example above should cover the most relevant plot options.