Measurement
General principle
To calculate the age of the sample two values are needed. The first one is the dose rate and the second one is the equivalent dose. The dose rate is calculated as follows:
\(\dot{D} = (\dot{D}_{\alpha}W + \dot{D}_{\beta}W + \dot{D}_{\gamma}W) + \dot{D}_{cosm}\)
where
| \(\dot{D}:=\) | Dose rate |
| \(\dot{D}_{\alpha}:=\) | \(\alpha\)-dose rate |
| \(\dot{D}_{\beta}:=\) | \(\beta\)-dose rate |
| \(\dot{D}_{\gamma}:=\) | \(\gamma\)-dose rate |
| \(\dot{D}_{cosm}:=\) | Cosmic dose rate |
| \(W:=\) | Water content correction factor |
For the determination of the equivalent dose, different techniques have been developed during the last years. The basic protocols are the additive- and the regenerative method.
Additive method
The additive method uses sub-samples of the original sample which are given different laboratory radiation doses and then their luminescence signal is measured. The luminescence intensity is then drawn against the added laboratory doses on a diagram. The function derived from the fit of the data points is extrapolated to zero luminescence intensity and the intersection point with the dose axis gives the equivalent dose.
 #### Regenerative method
#### Regenerative method
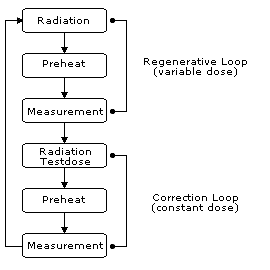
The SAR protocol (single aliquot regenerative) uses a single sub-sample (the expression aliquot is commonly used), from which the natural luminescence signal is measured. Then the aliquot is given different radiation doses, lower and higher than the expected natural accumulated dose, and measured again. To correct for sensitivity changes, in every irradiation-measurement-loop a correction step is integrated.

Calculation of the sensitivity corrected signal
\(\text{corrected signal} = \frac{\text{regenerative signal}}{\text{correction signal}}\)
Flowchart of the SAR-Protocol
Single aliquot regenerative (SAR) dose protocol usually applied on quartz minerals after Murray and Wintle (2000)